I want to take one image, chop it into square tiles, and use those to make an approximation of another image. When the images are the same size, the simplest version is identical to the assignment problem. This is a classical optimization problem that has been well studied. In those terms, there is a “cost” to placing a tile on the approximated image. This cost is a measure of how similar the tile is to the target image. We want to minimize the cost, but that gets computationally intensive when there are a lot of tiles.
If the images are both broken into N squares, then the cost for each tile-tile replacement needs to be checked, resulting in N^2 comparisons. The Hungarian Algorithm, one of the better algorithms for finding the optimal assignment, has a worst-case computational complexity of O(N^3). This gets expensive quickly!
Instead of doing this optimally, let’s approximate it greedily. For the first attempt, the idea is to grab a random unused tile, and figure out where it should be placed to minimize the error. Then repeat until we run out of tiles. This uses N*(N-1)/2 (basically N^2/2) comparisons, which is much faster than the optimal solution, especially when there are a lot of tiles. For this post, I’ll focus on the greedy method, but I’ll put some examples of the optimal results down at the bottom.
For the error metric, I’ll just use the squared distance between the average color of the two tiles. That’s illustrated below, where the source of the tiles is van Gogh’s Starry Night (left), the target image is the Mona Lisa (middle), and the mosaic is on the right.

Not a great start, but this is the very simplest method. The first major change isn’t to the mosaic algorithm, but rather to the brightness of the source image. Here’s the same basic algorithm, but with Starry Night modified such that its brightness histogram matches the Mona Lisa:

That helps significantly, since the output was lacking contrast. There’s still a lot of room for improvement. The next change is to compute the error as the total squared pixelwise difference, rather than the overall average. Second, allow for rotation of the tiles to make the edges more apparent. Third, pick tiles to initially fill the center of the image, and work outward. This helps put the well-matched tiles in the center, and the bad ones on the edges (where we don’t like to look anyway). The cumulative effects of each of those steps are shown below:

There’s a definite improvement! It’s recognizably the Mona Lisa, despite the shifted color scheme. Since we’re mixing fine arts, here are all the combinations of Starry Night, the Mona Lisa, and the Girl with the Pearl Earring.

Not bad! Well, the recreations of Starry Night are definitely strange. Too fleshy around the edges. One of the surprises that results from using a portrait as the tile source is that there are eyes hiding in the mosaics: near the top right of the Mona Lisa’s head, and at the bottom of the Girl’s head wrap.
To be fair, I should test out the optimal solution as well. Here are some examples of my greedy algorithm (left) versus the optimal solution (right).

As would be expected, the optimal case is better on average across the image, whereas the greedy method is better near the center. Here’s another example, where I use my temple image to recreate the Mona Lisa:

Similar conclusions as before, but much more stylized!
Just to be sure of the time complexity, I tested the two algorithms over a range of different numbers of tiles. With a lot of tiles, the optimal algorithm does seem to take N^3 time, and the greedy method takes N^2.
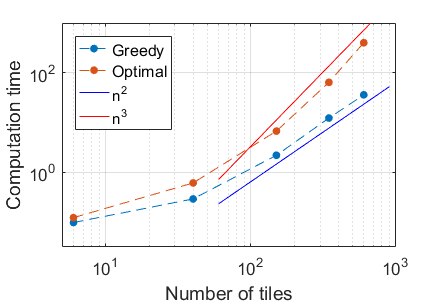
Optimality is expensive! In terms of the clock time, this could be sped up substantially, since the tile-to-tile comparisons are very parallelizable and I didn’t use any GPU functionality to take advantage of the parallelizability.
